
こんにちは! BolBolです!
今回は基本シリーズの第3弾です。
このシリーズでは、ボルダリングをするうえでぜひ押さえてほしい基本中の基本をご説明しております。
それぞれのポイントについて「なぜそれが妥当なのか」という理由を添えて、ロジカルにご説明しておりますが、結論だけを把握していただいても構いません。
いずれにせよ、ここでご説明する内容を参考に、上達のきっかけとしていただければうれしいです!
なお、シリーズ第1弾と第2弾の記事は以下のリンクからご覧いただけますので、より興味のあるテーマから先に見ていただければと思います!
それでは、はじめていきましょう!
”身体”の基本
第1弾は”手の使い方”を、第2弾は”足(脚)の使い方”を、それぞれご紹介しました。
そこで今回は、パーツではなく身体全体の使い方に関する基本事項を確認してまいります。
といっても。
実際のところクライミングにおける身体の使い方は非常に多彩です。

こうした多種多様な身体の使い方を網羅的に説明することは難しいので、あらゆる身体の使い方の大前提となる技術を1つだけご紹介したいと思います。
それは、身体のバランスの取り方です。
バランスの良し悪しによって、手や足(脚)にかかる負荷は大きく異なります。
どんなに手や足(脚)の使い方や筋力が優れていても、バランスの悪い状態で登ってしまっていると、クライミングの上達は困難なものとなります。
そこで、ここではバランスをとるための大原則を確認します!

回転運動と回転軸
さて。
いきなり物理の教科書っぽい見出しをつけてしまったので、学生時代の苦い思い出が蘇った方もいらっしゃるかもしれません。
しかしながら、ボルダリングにおける身体バランスの取り方を考えるうえでは、回転運動について理解しておくことが欠かせません。
そこで、今回は”回転”にまつわるごくごく初歩的な事実を確認するところから話を始めることにさせていただきます。
おことわり
回転運動を正確に考える場合、「力のモーメント」という概念を考慮する必要がありますが、今回は話を簡単にするために省略します。

さて。
ボルダリングにおける回転運動を考えるためにうってつけの構造物があります。
日常においても馴染み深いもので、その構造物とはドアです。

ドアは通常、戸の長辺を1組の蝶番(ヒンジ)で固定することによって、回転運動を実現しています。
ヒンジで固定された長辺が回転軸となり、回転運動が行なわれます。

そこで。
このような構造が手前にオーバーハングした壁に取りついていることを想像してください。
すると、当然ながら、重力が作用してドアは勝手に回転して開きます。
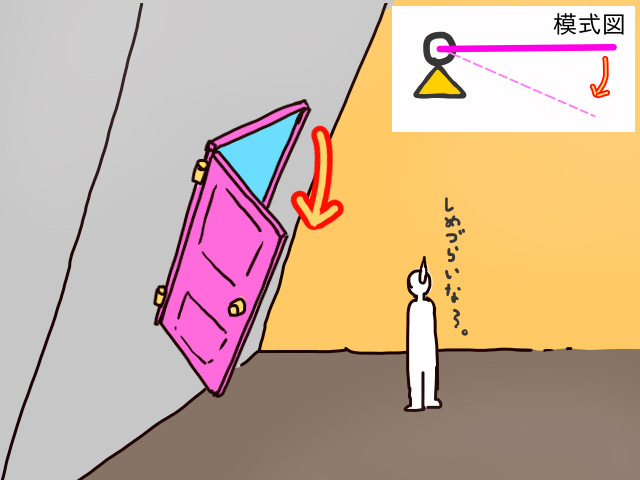
それでは、蝶番(ヒンジ)を釘に置き換えたらどうでしょう?
釘は蝶番とは違い、回転運動を許すような構造になっていないので、スムーズに回転することはありません。
しかしながら、この場合でも、ドアは重力の作用によって回転しようとはしており、釘は回転力に対抗しているため大きな負荷を受けています。
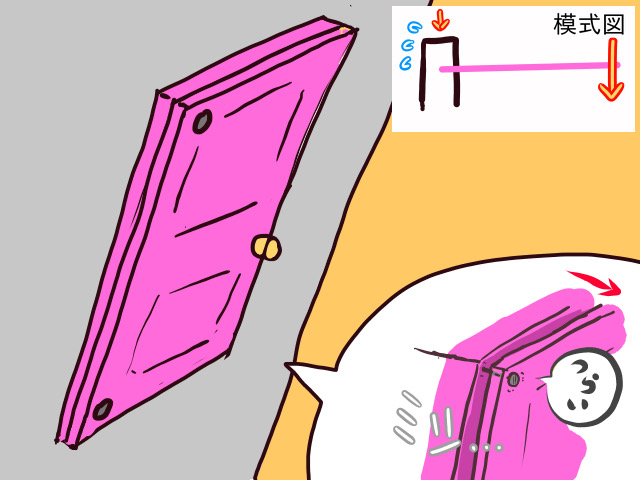
では、もしもこの2本の釘が長辺に偏らず、対角線上に固定されていた場合はどうでしょうか。
この場合、回転軸をまたいで左右対称になりますので、ドアが自然に回転することはなくなります。

すると、釘は回転に抗う必要がなく、ドアの重さだけを支えていれば良いために、負担は最小限度に留まります。
このような事情を踏まえて、話を次に進めましょう。
対角線支持の原則
それでは、以上の理屈をボルダリングに応用してみましょう。
次の画像をご覧ください。
右手を離しても大丈夫なのはどちらでしょうか?

正解は(B)です!
身体に働く回転力を考えるとわかります。

(A)は左手・左足で支持している状態です。
この状態だと左半身が回転軸になり、身体の重心はその右側に寄っています。その結果、左半身を軸としてドアのように回転してしまう構造になっており、そうした回転に抗うために右手に大きな負荷がかかっています。
よって、右手を離してしまうと、回転が始まってしまいます。

一方で。
(B)は左手・右足の対角線支持になっています。

回転軸を挟んだ両側の様子がおおよそ均等となり、結果として回転力が発生しません。
したがって、回転を止める力を使う必要がないぶん、右手にかかる負荷はより小さいものになっており、右手を離しても安定します。

これが、対角線支持の原則です。
一般に、対角線支持を実現する方法としては。
左手を離すときは左足支持
右手を離すときは右足支持
というふうに心がければOKです!

回転を利用して取りに行く技術
回転は避けるべきもの、というような伝え方をしてきましたが、意図的に回転を操ってホールドを取りにいく技術も存在します。
”ダイアゴナル”と呼ばれるムーブがそれです。

ただし、このときは「壁に近づくような回転」であることに注意してください!
さきほどの「ドアのような回転」の例では、「壁から剥がされるような回転」でしたから、この点が大きく異なっています。
なにより、”ダイアゴナル”を行なうときも対角線支持をしていることに注目してください!

あえて回転しようとするときでさえ、このような支持の仕方が有効となりますので、とくに初心者のうちはこの”対角線支持”を徹底するように心がけてみてください!
対角線支持の本質
ここまで、回転が生じる仕組みを踏まえたうえで、それを防ぐためには対角線支持が有効であることを確認してきました。
しかしながら、回転の仕組みを考えると、必ずしも支持点を対角線上に置く必要はありません。
本質的に重要なのは回転軸の両側の均衡です。
どういうことか、次のシーンをご覧ください。

この状態は左手・左足支持になっています!
しかしながら、右脚を回転軸の左側に大きく伸ばしています。
これによって、回転軸の両側の均衡が図られ、対角線支持ではないにもかかわらず回転力の抑制を実現しているのです。

ということで。
回転制御の要点は、回転軸の両側の均衡です。
対角線支持はこれを実現するための手段の1つであり、上記のような工夫もまた、そうした手段の1つであると言えます。
また。
このことがわかっていると、対角線支持をしているから絶対に安全とも言えないことがわかります。
次の画像をご覧ください。

この状態は左足と右手支点になっているので、紛れもない対角線支持なのですが、回転軸の右側に身体が寄りすぎているため、やはり回転してしまいます。
このような状態では、回転軸の両側が均等になるように体重移動を図る必要があるのです。

このように、回転力を制するための安定姿勢の要は、回転軸の両側の均衡であることを、ぜひとも心に留めておいてください。
まとめ
第1弾の「手の基本」、第2弾の「脚の基本」に引き続き、第3弾である今回は「身体全体の使い方の基本」についてご説明しました。
これにて、ボルダリングの基本シリーズはひとまず完結です。
たくさん説明してしまいましたが、ご満足いただける内容になっていたでしょうか。
言葉を尽くして丁寧にお伝えしたつもりですが、理屈っぽくて逆に混乱させてしまったかもしれません。
もしも理解に苦しむ箇所があるようでしたら、その部分については結論だけを把握していただいたうえで、ご自分で実践してみてご納得ください。
本シリーズでも繰り返しお伝えしておりますが、こうした理論は理解のきっかけや応用可能性を与えるものの、最終的に大切になるのは実体験に基づいて養われる”感覚”です。
なので、今回お伝えした内容を参考にしたうえで、ぜひとも実際に身体を動かして体感としてご確認ください!

また、こうした基本を踏まえたうえで、上達のためにはさらに高度な技術としてムーブを習得していく必要があります。
こちらの記事でご説明していますので、ぜひ合わせてご覧ください。
なお、冒頭でもお伝えした本シリーズのバックナンバーはこちらからお願いします!
最後まで読んでいただきありがとうございました。
それでは、ガンバです!
提供:ボルダリングジムBolBol






